Single-cell RNA sequencing has allowed us to capture the functional state of a cell at an instant in its lifetime. What makes this representation of cell state so powerful? The key is that it can be used to determine a cell’s relationship to other cells and cell states. Researchers have mainly probed this relationship in two ways: by clustering cells into discrete subpopulations based on the similarity of their expression profiles, or by situating cells along a data manifold. A manifold is a compact representation of high-dimensional gene expression data in a much lower-dimensional space that preserves relationships, or data topology. It is better at depicting continuous biological processes such as differentiation or immune cell activation. 

By imagining a walk along the manifold, it’s possible to order cells along an inferred trajectory—from an early stem-cell state, say, to a terminally differentiated state. It is remarkable that a progression of cell state transitions can be inferred from a lone snapshot of a sequenced sample that contains a mix of cells at different stages. What’s more, this can be achieved with minimal prior biological knowledge. 

Our group pioneered efforts to learn trajectories with the Wanderlust algorithm, which was originally developed for single-cell mass cytometry data. We next developed Wishbone, which introduced a single branch in the trajectory, and could be applied to single-cell RNA-seq data. Around that time, the field became intensely focused on branching, driven by the idea that what happens before, during and immediately after a branch point is key to what informs cellular fate decisions. It was assumed that decisions would be understood better if they were pinpointed more accurately.

We also dove into this quest and attempted to build a generalization of Wishbone: an algorithm that would automatically determine the number of branches in a dataset and their relationships, using a starting cell identified from known biology. We used data from hematopoietic stem cells—blood and immune progenitors found in bone marrow. But the harder we tried to accurately localize branchpoints, the more we realized that our efforts were not robust.

Our failure forced us to stop and listen to what the data was telling us.

Whereas cell fate decisions have been modeled as discrete and binary, we realized that, like cell state transitions within a lineage, a cell’s fate choices are probabilistic, continuous entities. Framing the problem this way immediately opened new possibilities. 

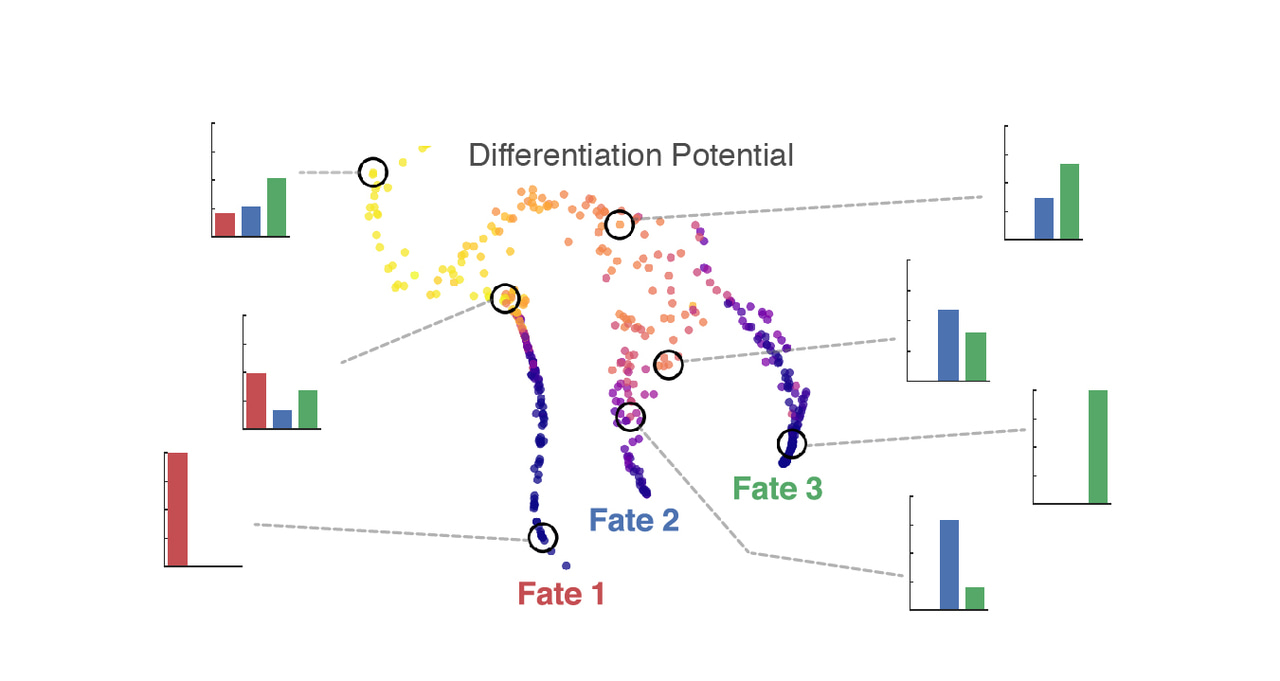
Palantir models a trajectory as a Markov process, a probabilistic model of change over time. The algorithm identifies terminal states in a system, and for each intermediate state, it learns a set of probabilities for reaching each terminus. Each cell or cell state is thus associated with a corresponding vector of ‘branch probabilities’. These probabilities can in turn be summarized using entropy, which we showed is equivalent to the cell’s differentiation potential—a core concept in developmental biology. 

Applied to a human hematopoiesis dataset, Palantir correctly determined terminal states and differentiation landmarks, and allowed us to identify decision-making regions as well as to recognize lineage-specifying genes by their involvement in altering differentiation potential. We also showed that generalized additive models are a powerful way to characterize the expression dynamics of genes such as transcription factors along trajectories. Using epigenetic and target gene expression data, we confirmed Palantir’s prediction that a drop in the ratio of PU.1 and GATA2 activity precedes erythroid lineage specification. The algorithm seamlessly generalized to mouse hematopoiesis and colon differentiation data.

Like all trajectory methods, Palantir assumes that differentiation is unidirectional. This assumption is often violated in regenerative or disease settings such as cancer, which may require additional information about cell lineage to model. Palantir also relies on the manual selection of an approximate starting cell based on biological knowledge; however, the algorithm is robust to the exact start location, and it can determine the start automatically if terminal states are known.

Modeling cell fate choice in a probabilistic way has made it possible to quantify differentiation potential, which is critical to understanding how cell fate changes are regulated. This adjustment in our way of thinking only came about because we stepped back to really appreciate what the data was telling us about cell behavior.

Manu Setty, Tal Nawy and Dana Pe’er

Setty M, Kiseliovas V, Levine J, Gayoso A, Mazutis L & Pe’er D. Characterization of cell fate probabilities in single-cell data with Palantir. Nat. Biotechnol. 37, 451–460 (2019). Read the paper here.